Lecture 3: Bits and Bytes; Bitwise Operators

All data stored in memory (in whatever format) is ultimately stored in binary. So it is important to learn about how we can manipulate this binary code which is what we will discuss here. As an example, take int x = 5;. In binary this is roughly 0b0…0101. Usually, we can just manipulate x in high-level code. But here, we will learn to manipulate the underlying binary representation. The advantage of this is efficiency (storing data, arithmetic, etc.).

Now that we understand binary representations, how can we manipulate them at the bit level?

Bitwise Operators

We are all familiar with our regular operators we use in high-level programming languages (HLPL) such as logical (&&, ||, !) and comparison (==, !=, <, >, <=, >=). We now introduce a new category of operators:

❕
Bitwise operators: &, |, ~, ^, <<, >>

You can think of 1 as representing "on" or "true" in regards to the comparison or logical operators and 0 as "off" or "false".

You can also operate on more than one bit at a time. Below, two nibbles are operated on for each one. The output is produced column-wise.

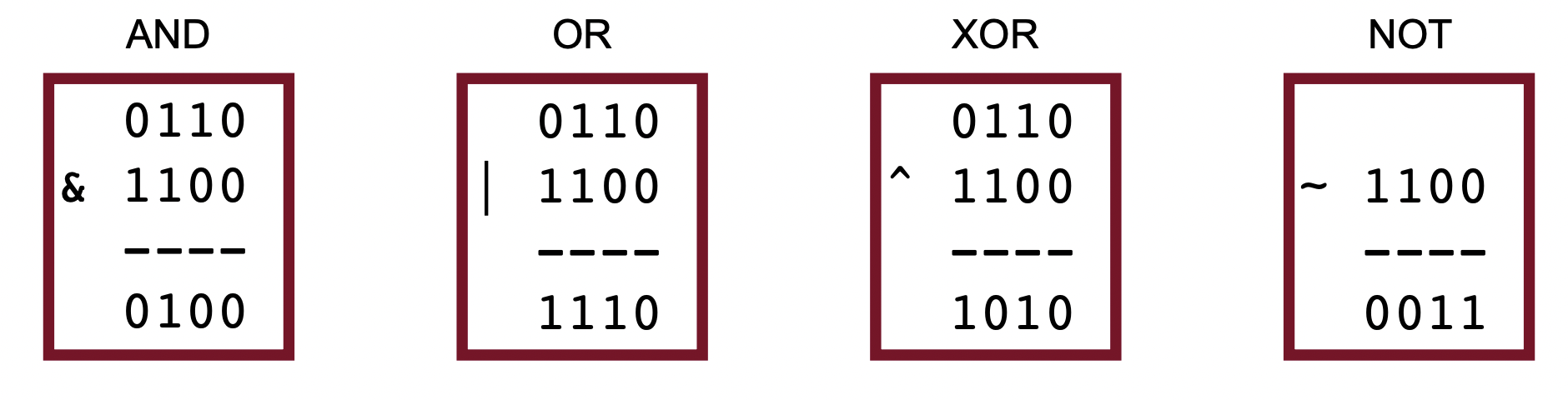
There is also an important difference between HLPL logical operators and bitwise operators. Bitwise operators result in some binary output so the operators themselves can be used for manipulation and produce a desired output (see the section on bitmasks below). For example, if you want to invert a bit, you can simply apply the ~ operator and a binary representation will be outputted—not simply just a "True" or "False". Additionally, you should be able to differentiate between HLPL operators and bitwise operators solely based on the symbols representing the operators themselves (i.e. & is bitwise and && is HLPL). This is because you could be given questions like 4 & 5 and 4 && 5 which produce different outputs (the former one is bitwise so you should convert the 4 and the 5 to binary first).

Bitmasks

We talked previously about how one of the incentives for representing data at the bit-level is efficiency for things like storing data. Here we present:

❕
Bitvector: ordered collection of bits to represent sets

With these bitvectors, we can perform set notation operations such as union.

So how would this be more efficient? Say we want to keep track of courses taken for a student. In HLPL, we can make a data structure composed of true/false values for each course. This would be 8 bits for each value so 64 bits in total. However, in binary, we can represent each value is a bit itself which leads us to using only 8 bits which in an HLPL, we can represent using the corresponding char.

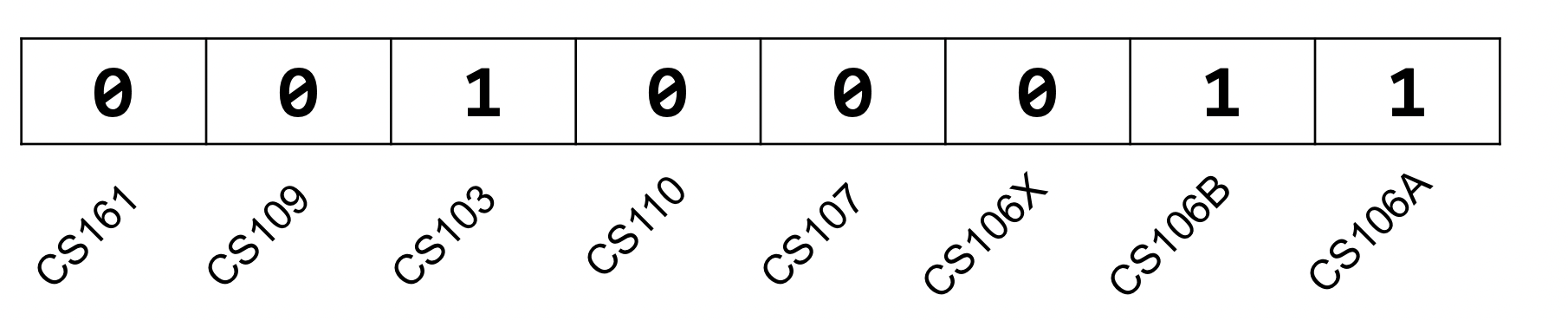
So we know we can manipulate bits using bitwise operators. Let us say we want to manipulate the above bitvector such that CS 107 is turned on. What we do is construct a bitmask.

❕
Bitmask: A bitmask is a constructed bit pattern that we can use, along with bit operators to manipulate or isolate out specific bits in a larger collection of bits.

For example, we can construct the bitmask 0000100 and use the | operator to turn on CS 107 in the above bitvector. We would get 00101011 as an output. We can also literally define a constant for these bitmasks in a low-level programming language and then work with that constant to manipulate. It is good practice to play around with these operators and bitmasks. Here are some common tricks and tips:

GDP

❕
GDP is a command-line debugger that lets us step through our programs and print out values (even at the binary level) at different places.

To-do: take notes on the debugger demo video (3.3)

Powers of 2