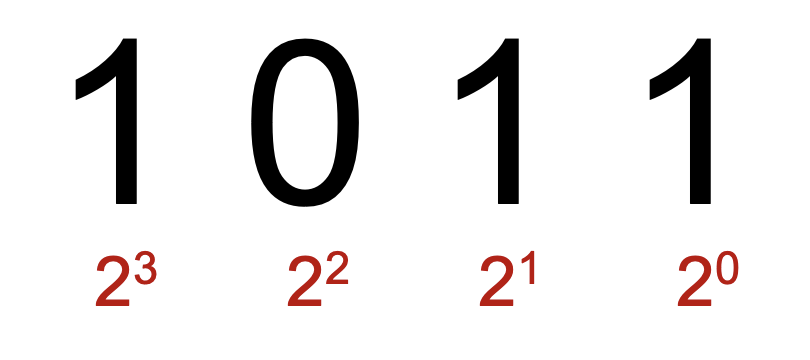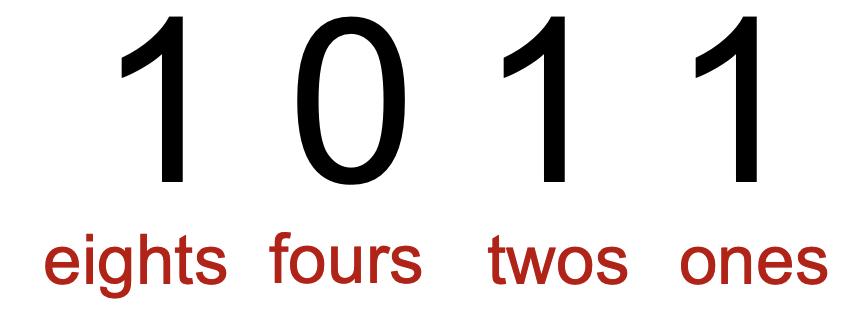Lecture 2: Bits and Bytes; Integer Representations

Table of Contents:

Topic: How can a computer represent integer numbers?

Bits and Bytes

❕

Bit: a bit is either a 0 or 1. It models state ("on" or "off").

Bits are modeled in software using 0s and 1s whereas in hardware, they are transistors on a chip.

Since one bit doesn't allow much space, we can combine bits to form a byte:

❕

Byte: a group of 8 bits. A nibble is a group of 4 bits.

Computer memory is simply a giant array of bytes (can't store at the bit level). We access the computer memory (called a stack or heap) via addresses written in Hexadecimal.

So how can we represent data (specifically we will talk about integers in this lecture) in computer memory? The goal is to fundamentally understand how all of the high-level functionality of a computer can be translated down into the lowest level: 0s and 1s.

For integer representation, we will study number systems of different bases. Of course, the fundamental one is base-2 which is binary because binary represents the 0s and 1s.

Base 10

This image sums up the number system we are all familiar with.

Base 2 (Binary)

Ahh... binary. We will work a lot with binary in this class so be sure to become familiar with it now.

We can think of the places in a binary number as powers of 2 (hence why we call it base-2).

\rightarrow

We can harness this intuition to convert back to base 10 (base 2 to base 10):

1^{*} 8+0^{*} 4+1^{*} 2+1^{*} 1=11_{10}

Essentially, we take the index's number place (e.g. ones, twos, fours, eights) and multiply it by the digit (0 or 1) at that place and sum up for each place.

In base-2, the most-significant bit is the one furthest to the left and the least-significant bit is the one furthest to the right.

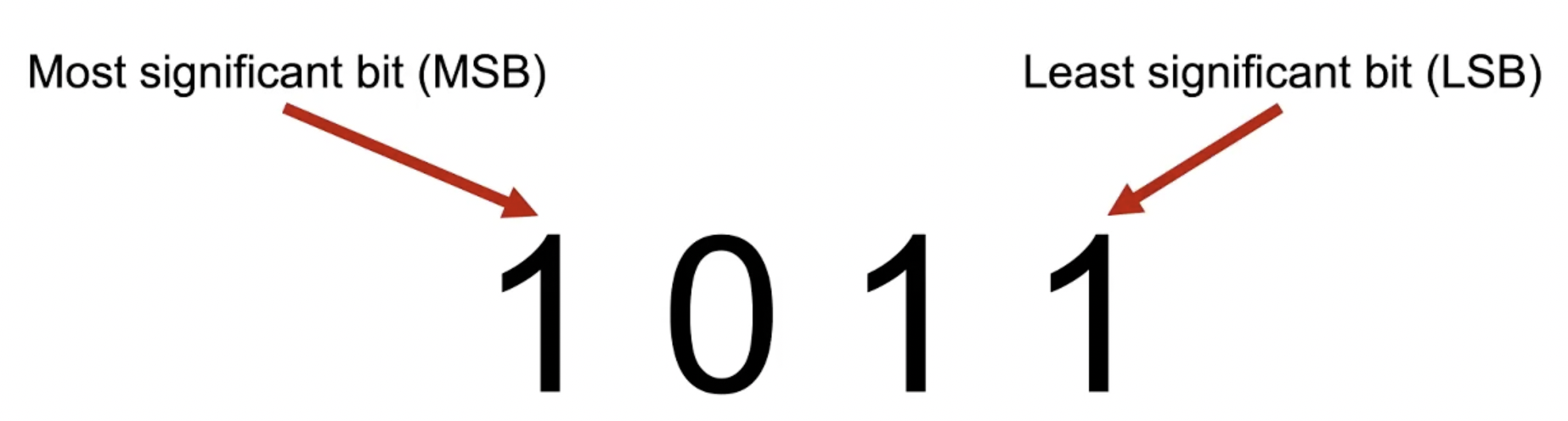
Base 10 to Base 2

B10 to B2 is a bit more tedious than the other way around (as described above). The strategy you want to use is as follows.

You want to ask yourself what is the largest power of 2 that is less than or equal to the base 10 digit you are trying to convert to base 2. Repeat this process until done.

For example, if you have the number 6:

2 to the power of 2 is the largest power we can use to remain $\leq 6$ : $2^2 \leq 6$ . $2^2$ is equal to 4 which means we place a 1 in the fours place of the binary digit.

Now we ask: what is the largest power of 2 that satisfies $2^x \leq 6 - 2^2$ . The answer is $2^1$ . $2^1$ is equal to 2 which means we place a 1 in the twos place of the binary digit. We have accounted for everything in the number 6 so we now place 0s everywhere else: 0110.

Not relating to this specific subsection, but best placed here, multiplying by the base in a base number system adds a 0 to the number. For example, 10 * 10 is 100 which adds a 0 in base 10. Division removes a 0.

Hexadecimal

Base 16.

For each nibble in binary: we take up 4 digits. We have 16 possible representations of base-10 digits (0-15). In hex, the numbers 0-15 using only one digit:

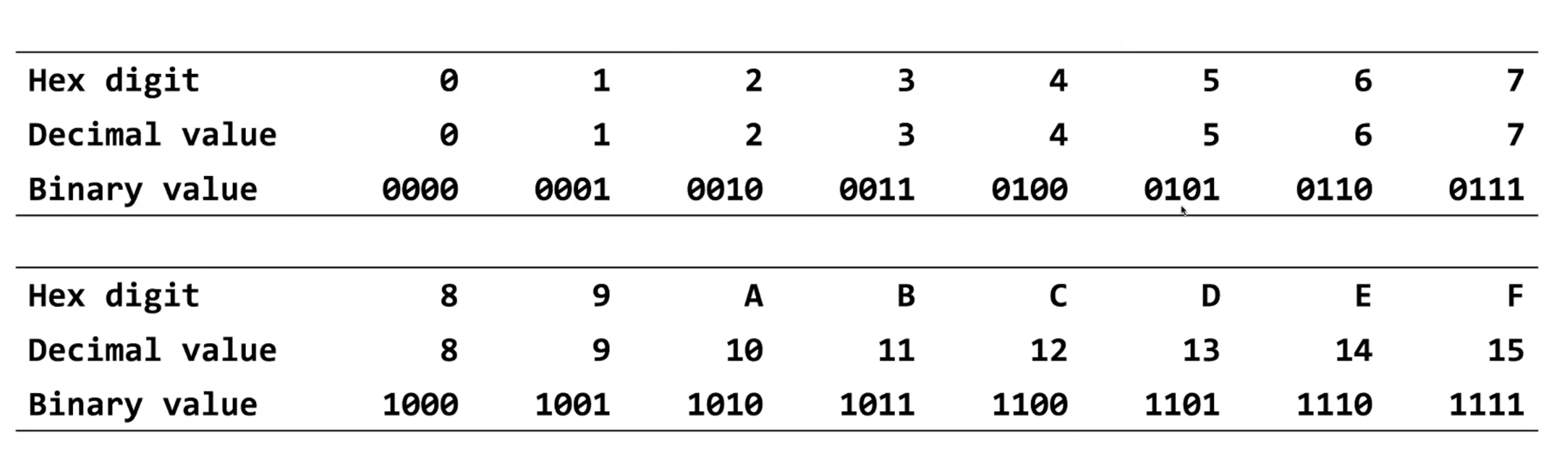
This is also useful because some 32 to 64 bit binary numbers is way too cumbersome to perform calculations on.

To convert from hex to binary (or vise versa), simply use the map above (one hex digit should result in four binary digits). Start from the right for binary to hex (and fill in any leading zeroes for making the conversion easier).

Prefixing

So how do we know what number system a digit belongs to? We use prefixes.

0b for binary (e.g. 0b1010).

0x for hex (e.g. 0xf).

Integer representations and unsigned integers

Now that we understand fundamental number systems, how can we represent integers under the hood in a computer? Everything needs to come down to binary eventually. We will look at unsigned and signed integers.

❕

Unsigned integers: A positive (or 0) integer (no negatives).

Fortunately, unsigned integers in base-10 convert to binary in the same way as we learned about above—it is a simple 1:1 conversion.

Now what about negative integers? For that we have:

❕

Signed integers: A positive, negative, or 0 integer.

So how can we represent both negative and positive numbers in binary?

One idea is...

Sign magnitude representation

The idea is to allocate the most-significant bit to represent the sign.

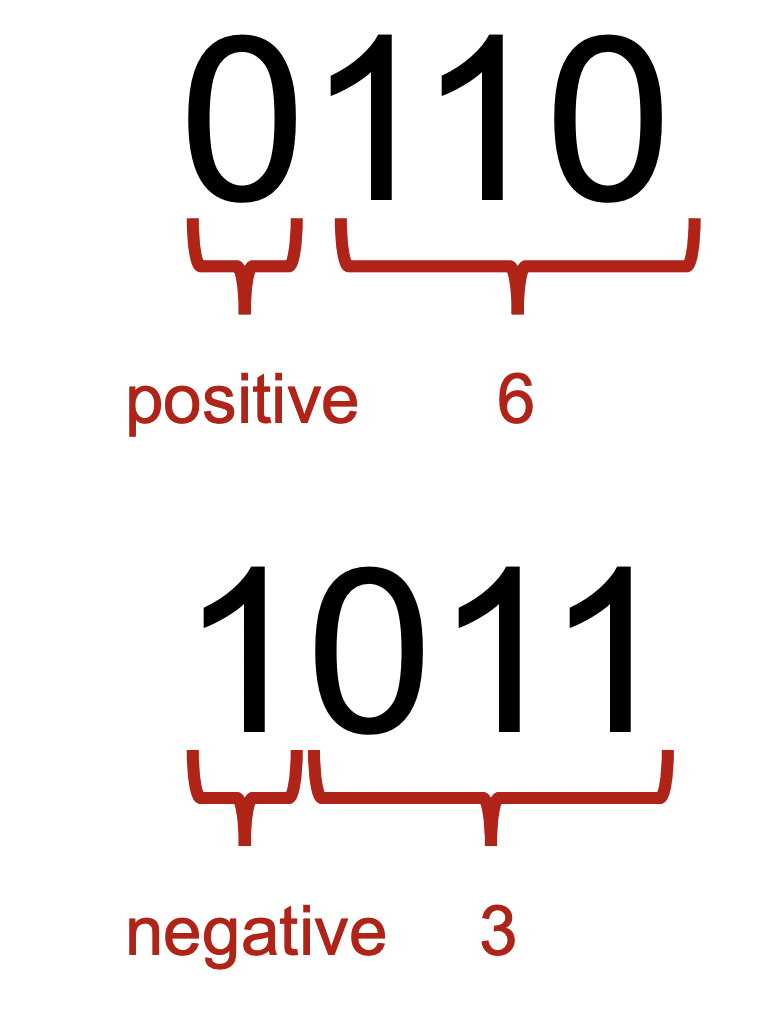
A problem arises because we now have both a positive and negative representation of 0. Another problem is that it takes one more bit than necessary to store a number. Arithmetic is also trickier in this representation.

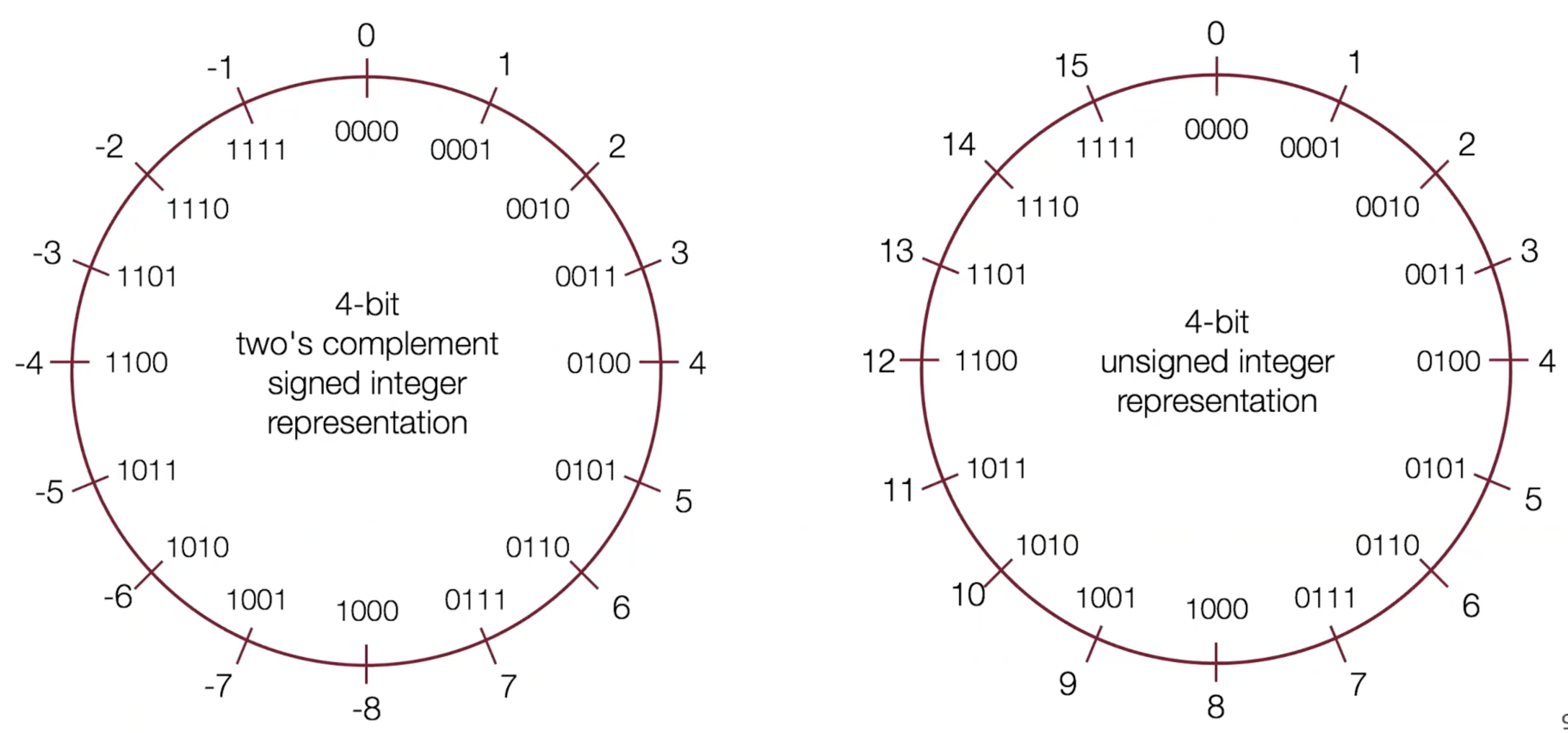
Two's compliment

So how can we fix the shortcomings of sign magnitude representation? Through the two's compliment system.

Before we get started, it is important to note something about binary addition. What even is binary addition? Well it is the same as adding up any kind of number the grade school way with one small caveat. We can only get a binary number that results in 0s and 1s. So if we have a result that equates to > 1, we carry the 1 over to the next place. If this occurs in the most-significant bit place, the 1 falls off the edge and the result in that place is a 0.

In this system, we can map each positive number to its corresponding negative number while retaining the same number of bits. The algorithm for yielding a positive's number's negative compliment is as follows:

Invert the binary number.

Add 1 to this inversion.

The pattern is that we want a positive number plus its negative number to equate to 0. Inverting the binary number makes the sum all 1s. Adding 1 to this makes all of the 1s fall of the edge so we end up getting all 0s.

All of the cons from sign magnitude representation become pros in two's compliment. Specifically, arithmetic operations map to what they would equal in base-10.

Overflow

Remember how we talked about how adding 1 to a number sometimes results in the 1 falling off of the edge? Formally this is called overflow.

❕

Overflow: If you exceed the maximum value of your bit representation, you wrap around or overflow back to the smallest bit representation.

For example, say we allocate space for a 4-bit number (in practice, we have data types (e.g. int, long, short) that all have min and max values based on how much bits they take up). We initiate that number with the binary digit 1111. If we add 1 to it, we would get 10000, but we only are allowed 4 bits. Thus, we have an overflow and we wrap around to the smallest 4-bit representation which is 0000.

This holds for reverse: min - 1 wraps back to max.

Casting and Combining Types

One thought you might have had in discussing the two's compliment system is that there may be a binary number that represents what it represents but also some other unsigned number equivalent. Thus, in practice, we must specify the type (whether it is unsigned or signed) when working with integers. Examples (look at left-hand side).

When comparing integers, if the integers are of same type, the comparison happens as usual. However, if one is of unsigned type and the other is of signed type, for the purposes of comparison, the signed one will be casted to unsigned and then compared.

Sometimes we will also want to compare integers that are of two different data types (i.e. short and long). We can cast the short to the long to do the comparison. In doing so, in binary, we add leading zeroes if the short is unsigned. For signed, we add either leading 1s if negative or 0s if positive.
- It is dangerous to go from a big to small data type. C truncates the most significant bits.

We can use the sizeof() command in C to get the amount of bytes of a certain data type.