Lecture 17 TLDR: Regular Expressions

• We will focus on the building up regular languages from smaller ones via closure properties.

• The way we do this is via regular expressions.

Regular expressions are a way of describing a language via a string representation.

Atomic RE's

These are the fundamental units to which we can build every language from:

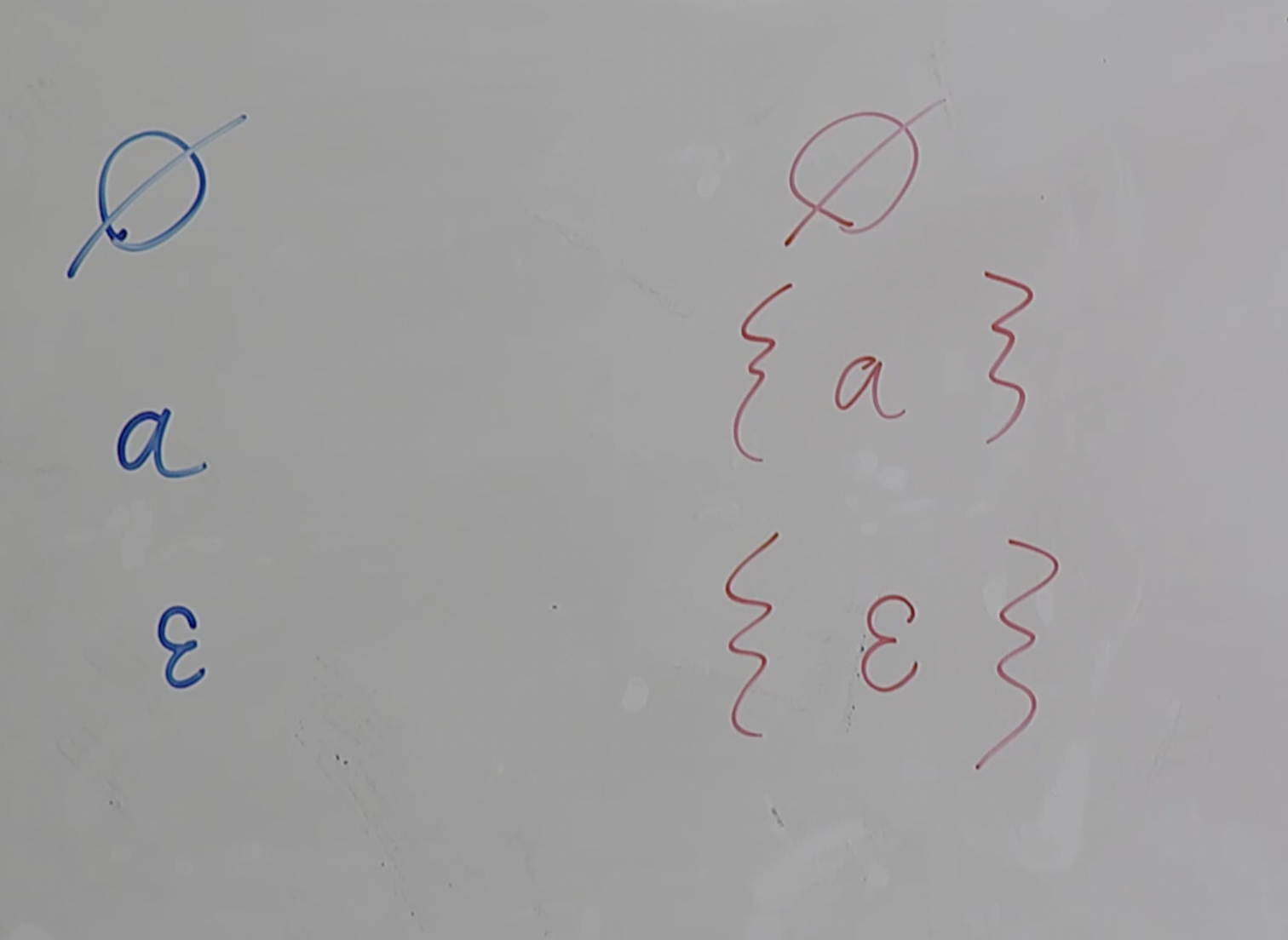
Closure properties (compounding)

Three closure properties (everything else is a derivative):

• Can compound these atomic units to form larger expressions by concatenating them. Example:

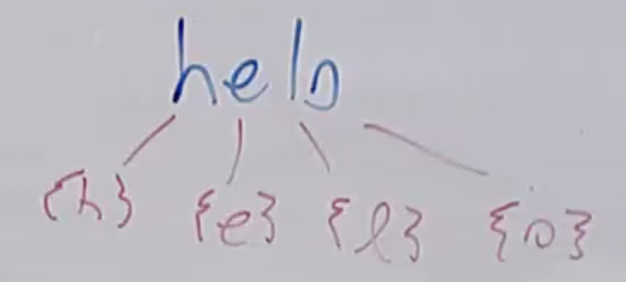
Other compounding actions are through the following properties.

• Union

• Kleene's Closure

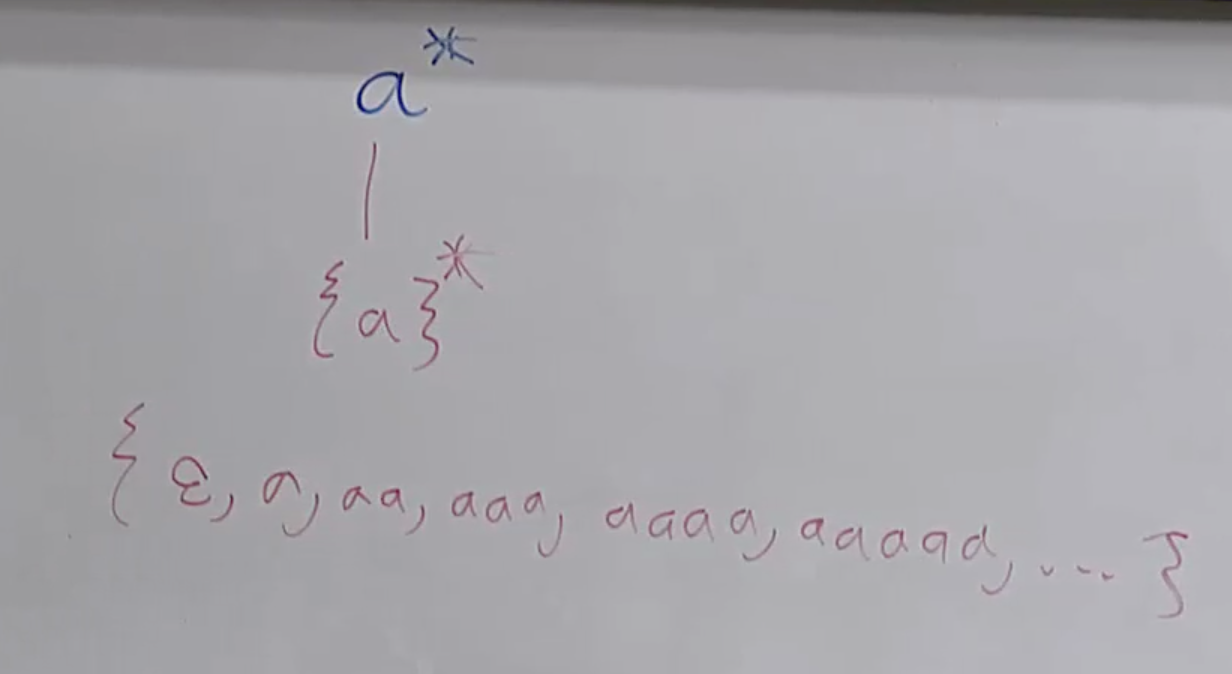
Operator precedence

Remember, RegEx is a string representation of languages. It evaluates like a mathematical expression so we need some order of precedence which we define as the following:

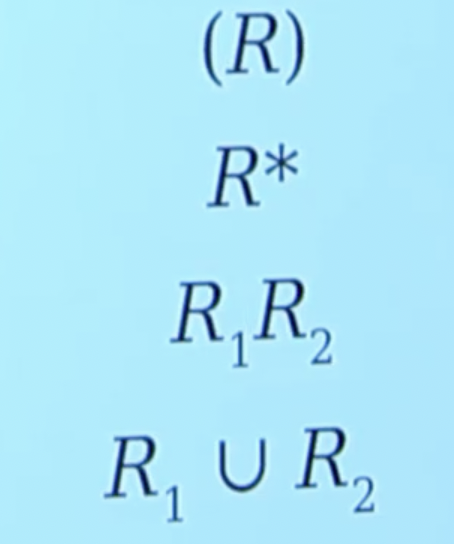
Example:

Also important to realize that RegEx closure operators operate via individual characters and not the entire string. For example, in $boo^*$, only the last o can be kleene starred and not the whole string.

Designing RegEx's

Can also design them from alphabets and languages (see 30:00). Here is an example:

See middle of lecture for more examples.

Some more notation

• Note something: $EEEE$ can be written as $E^4$.

• Another new notation: we can implement "optional" characters via the $?$ notation (meaning choose if you want). Example: $b^{*} a ? b^{*}$ where $a$ is optional.

• Kleene plus operator: $a^+$ means "one or more $a$'s".

Some results (proofs)

We also have another result which is the reverse (which isn't as obvious):

Why so:

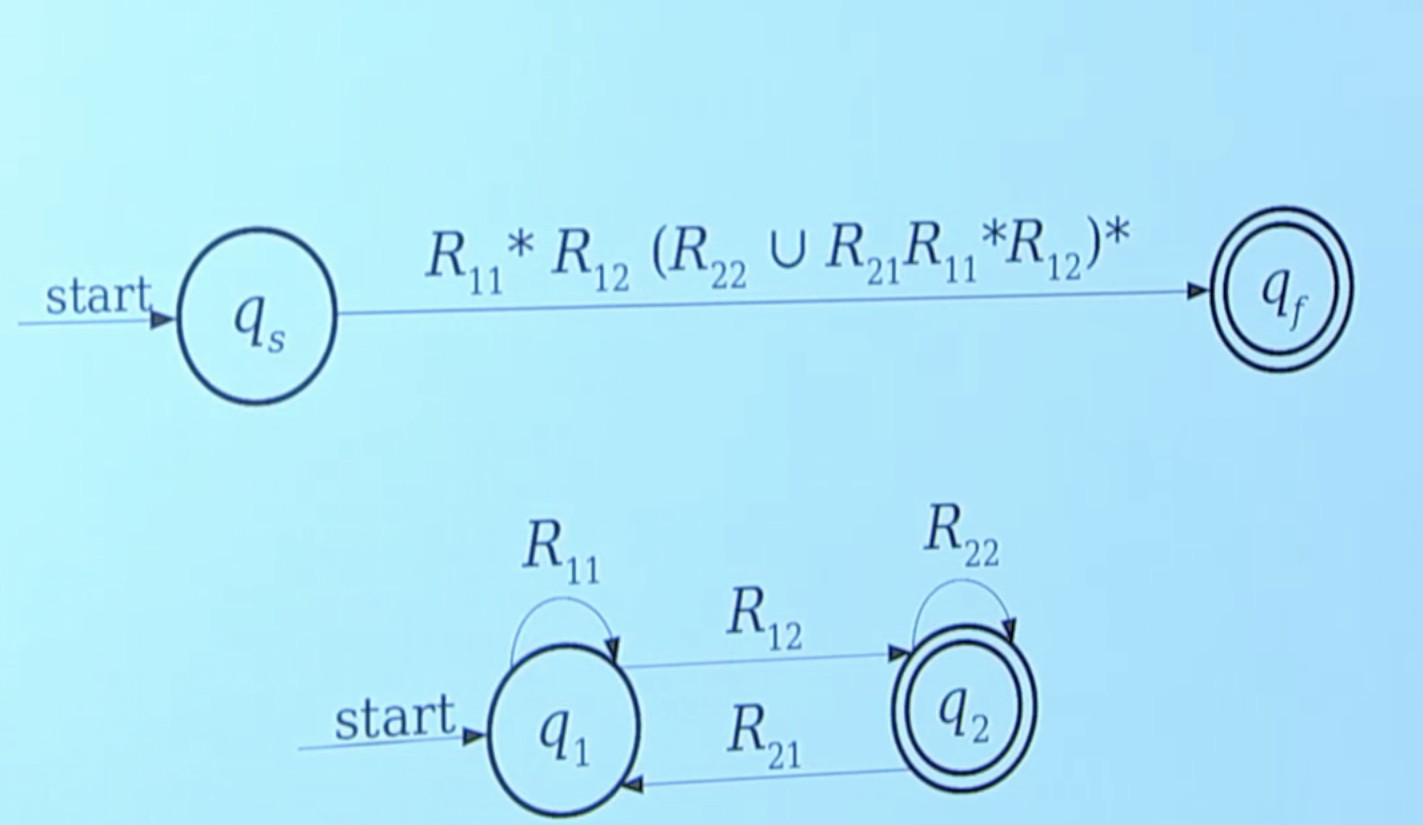
• We only have three atomic units with three basic operators when working with RegEx's so if you have some complex finite state machine, then it can be very hard to pull out an RegEx out of your hat. Though, by theory, this should be possible since RegEx's represent regular languages in string form.

Essentially, the proof would use this intuition:

More so:

• Notice that all transition labels of an NFA sort of function like RegEx's.
  • As a thought experiment, label all transitions with RegEx's (which isn't legal though, but hypothetically think).

• Then, somehow get your NFA to be of one transition and two states:

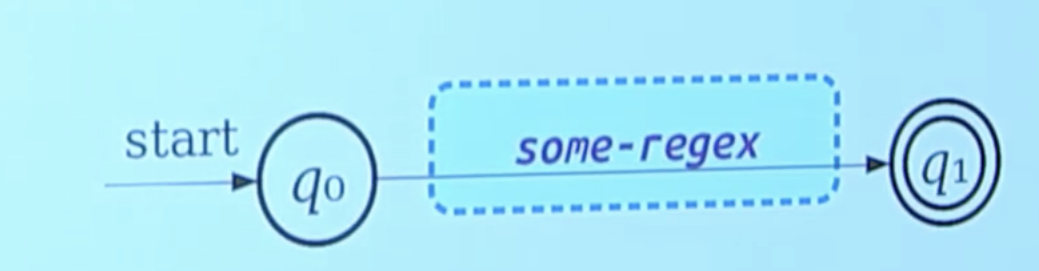
One tip: self-loops are "stay here as long as you like" and in RegEx form, we use the Kleene operator: $a^*$

A complete example of this theorem: