Lecture 14: Automata

Date	@May 12, 2021

Introduction

For introduction to FSA's, view the relevant section in this PDF:

https://s3-us-west-2.amazonaws.com/secure.notion-static.com/5e0c7448-83f3-4fcd-8af0-fe16d7e2df1c/main.pdf

Briefly summarizing:

Computability theory revolves around the question: "What problems can we solve with a computer?"

To formulate mathematical proofs for what we can and cannot solve with computers, we need a general purpose model of a computer that represents any form of a computer.

As such, we have automata which are mathematical models of computers.

Finite Automata

A finite automaton is an automaton which a limited amount of memory.
- Formally "Finite automata are an abstraction of computers with finite resource constraints."

There are also Turing Machines, which we'll discuss later on in the quarter that have an unbounded amount of resources.

Problems

To reason about the question "What problems can we solve with a computer?", we need to formally, and mathematically, define what exactly a "problem" is.

Preferably, we want a definition of a problem that:
- Corresponds to the problems we want to solve,
- *Captures a large class of problems,
- *Mathematically simple to reason about.

However, no one definition perfectly covers all three. We'll mainly focus on the last two (starred).

Formal Language Theory

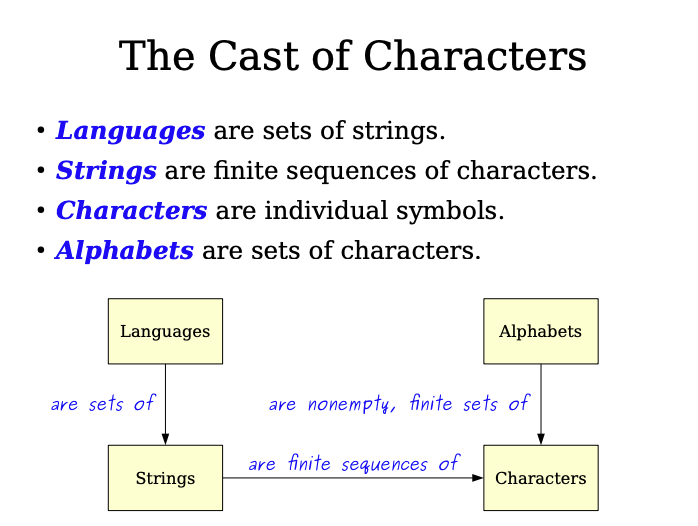
Alphabet: a finite and nonempty set of symbols called characters.
- Defined using $\Sigma$ .

A string over an alphabet $\Sigma$  is a finite sequence of characters drawn from $\Sigma$ .

We can also have an empty string which is symbolically represented as $\epsilon$ .

There is also $\in$ which is "element of" like in set theory notation.

So what is a language?

A formal language is simply put "a set of strings".

More so, we say that a language $L$ is a language over an alphabet $\Sigma$ if all of the strings in the language are over that alphabet.

Example:

Furthermore, we define $\Sigma^*$ as the set of all strings possible from the alphabet $\Sigma.$

This allows us to mathematically define a language as:
$L$ is a language over $\Sigma$ if $L\subseteq \Sigma*$ .

So essentially, a language over some alphabet is simply some set of strings over the alphabet which is a subset of all possible strings from that alphabet.

So in summary:

Finite State Machines

Back to the question of computability theory, we say that a "problem" is just some formal language.
- Now you might be thinking how the heck we represent problems by using a formal language. This is best explained through an example: say we had the problem of identifying if a mathematical expression is correct. We can define some language which contains all the correct mathematical expressions and then simply check to see if the given expression (which would be represented as a string) is indeed in the language.
- Formally: "Given a string, is such a string contained in the stated language?".

Now how can we define some "computer" to solve these problems (or not)?:

A finite automaton is a simple type of mathematical machine for determining whether a string is contained within some language.

An FA has these things called "states" which are connected through these things called "transistors".

They look like this:
Nodes are states. Transistors are edges.

There are two special types of states:
- Start state
- Accept state (noted by double ring)

Note that you can also have this thing called a "sigma" transition which is represented by $\Sigma$ and means the total alphabet.

Given some language, you travel along the FA, starting at the start state, and if you end up at an accept state, then you "accept" the input string.
- So in some sense, there is this mechanical tracing process you follow (it is like a guided maze!).
  - See (35:00) for how to trace.

Summarizing thus far:

Designing Automata

You would ideally want to design your automata such that it answers the problem you are working with.

We introduce the notion of a "language of an automaton":

A language of an automaton is the set of all accepted strings of that automaton

Note: remember that we operate over strings when tracing through automata. The language is a set of all possible strings that would be accepted.

Formally, we define such as:

If $D$ is an automaton that processes characters from the alphabet $\Sigma$ , then $\mathscr{L}(\boldsymbol{D})$ is formally defined as

\mathscr{L}(\boldsymbol{D})=\left\{\boldsymbol{w} \in \boldsymbol{\Sigma}^{*} \mid \boldsymbol{D} \text { accepts } \boldsymbol{w}\right\}

So ideally, if we were designing automata for a particular, we'd need to align $\mathscr{L}(\boldsymbol{D})$ with the accepted answers to the problem.

Ok but like how do you methodologically design an automaton?

A good intuition to have is to simulate the functionalities of memory. FSA's don't have any memory, but using some clever tricks we can simulate it.

Best explained through example:

Say you have this language in which you need to define some automaton for:

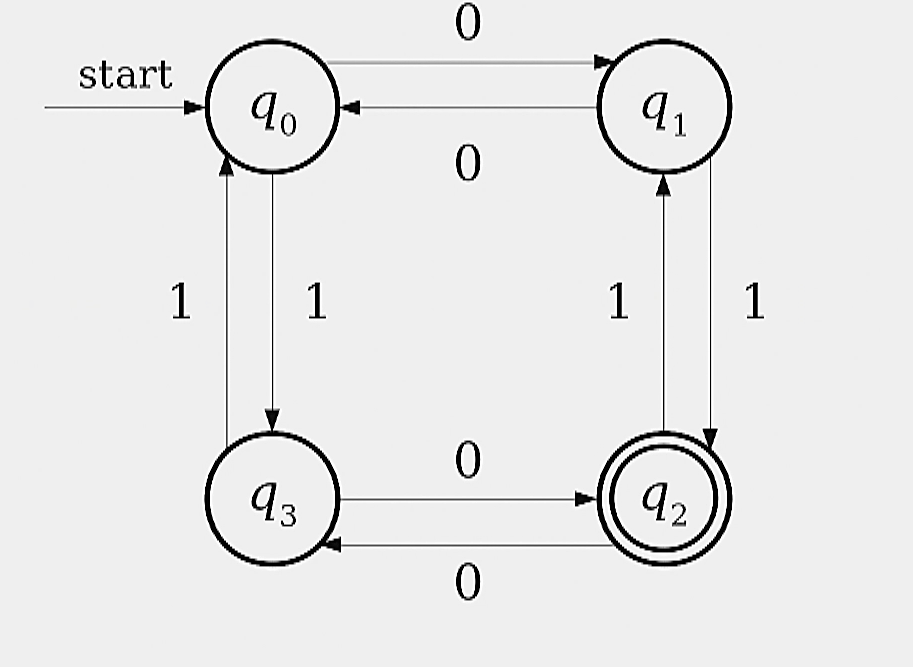
This is saying to design an FSA which only accepts strings from $\Sigma^*$ which contain a number of b's that is congruent to 2 mod 3. We design the FSA as follows:

We keep track of b's by moving one state (see how we are keeping track of memory?).

If the current character is an a, then we self-loop so it is not "counted" in our memory system.

We also only have a finite (hence "finite" state machine) number of resources so we loop around past the accepting state.

Overall, it looks like this:

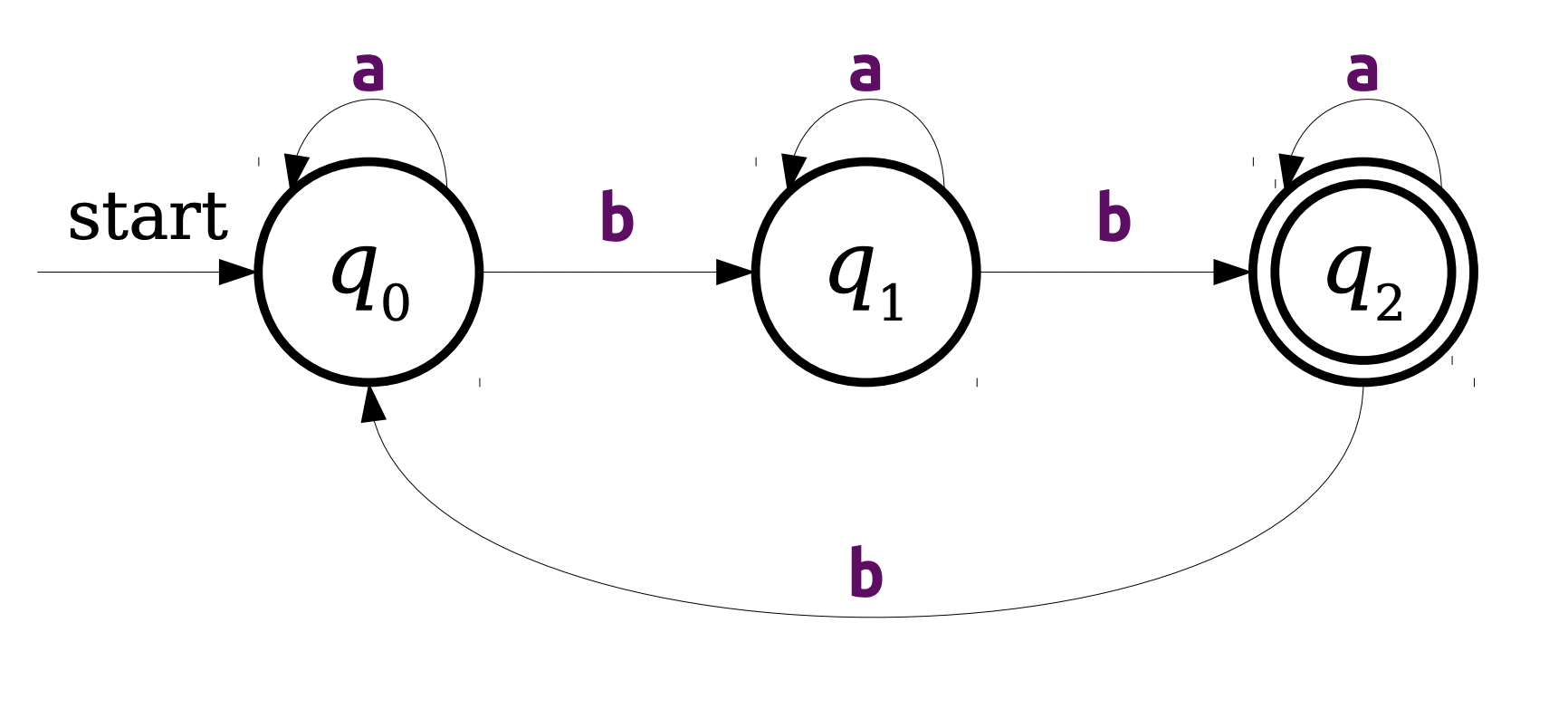
View the last minutes of lecture for a visual explanation.

Determinism

Consider a case where you have this automaton:

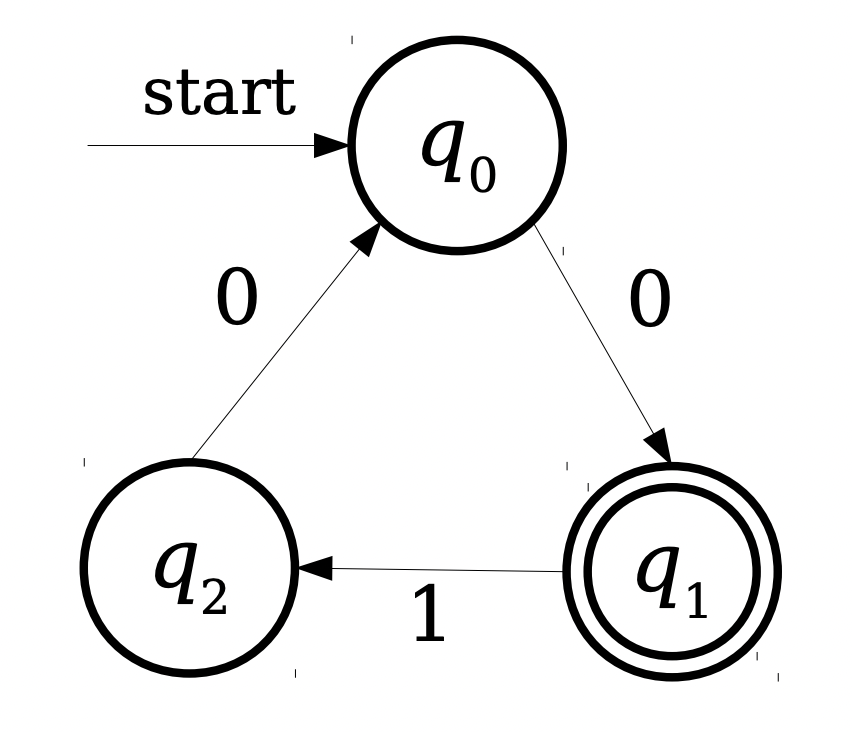
Notice that there are transitions that don't include 1s or 0s transitions in certain directions. This is a problem in regards to what we know so far. What would you do if you started with a 1?

More so, consider this automaton:

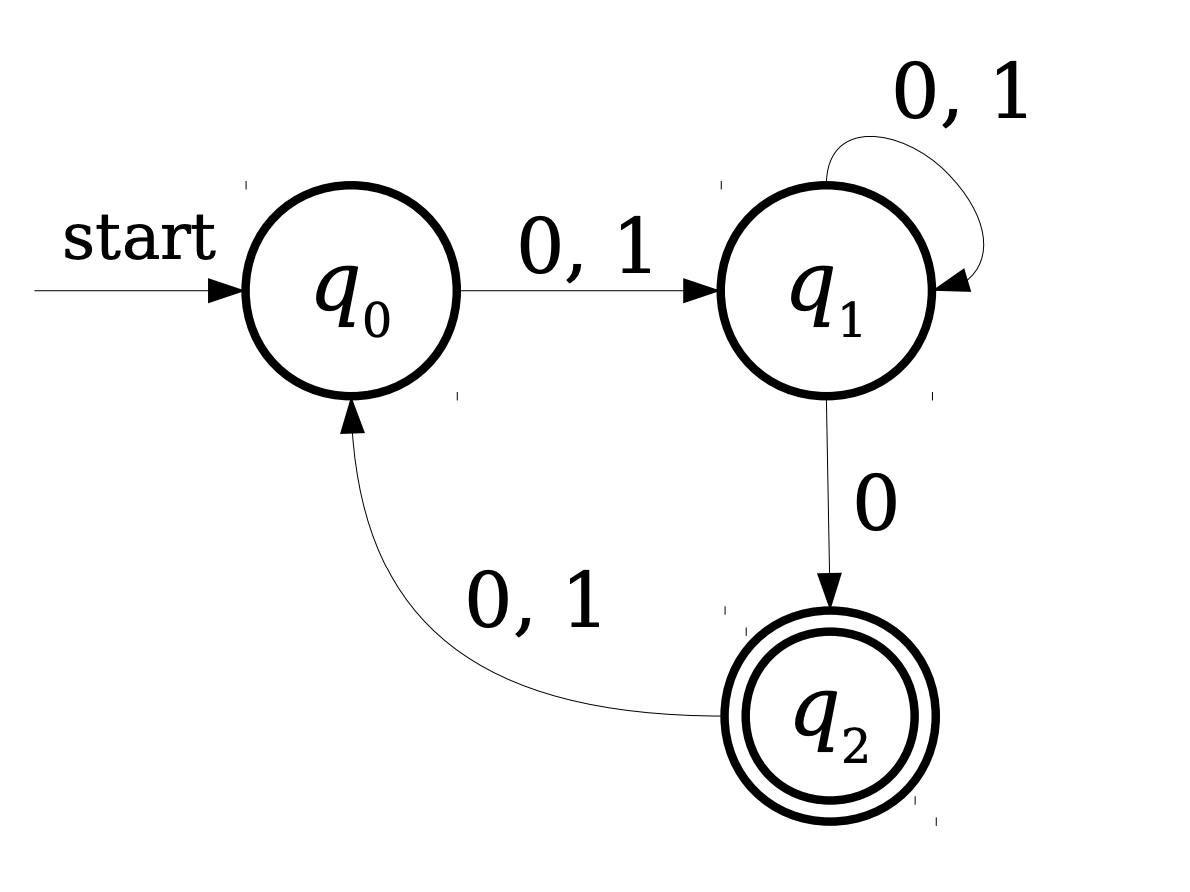
Notice that on the q_1 state, there would be two options for 0.

These two particular automata fall under the category of "Nondeterministic Automata". We will discuss these later on. In this particular lesson and the next few, we only deal with Deterministic Finite Automata which don't have these problems. More specifically, we define a DFA as having the following characteristics: