Week 2, Lecture 1 - Transfer Learning + Start of Meta-Learning
Transfer learning
🍎 Transfer learning: Solve target task 𝒯 after solving source task(s) b 𝒯a by transferring knowledge learned from 𝒯a.
How is it different from mult-task?
- MT: solve multiple tasks (\(\mathscr{T}_1, \cdots, \mathscr{T}_T\)) at once: \(\min _\theta \sum_{i=1}^T \mathscr{L}_i\left(\theta, \mathscr{D}_i\right)\).
- TL: Solve target task 𝒯 after solving source task(s) b 𝒯a by transferring knowledge learned from 𝒯a.
- Assumption: cannot access data 𝒟 during transfer. (data is separate).
- Good to use TL over MT when
- More data in source task than target task
- Don’t care about solving tasks at the same time
- Pre-trained weights for source task are available (e.g., pre-training on imagenet)
- In TL, we don’t need to solve tasks at the same time… just adaption.
- In this sense: transfer learning is a valid solution to multi-task learning (but not vice versa).
- We can do multiple tasks in TL but MT doesn’t transfer represenations over.
Transfer learning via fine-tuning
Most common way to do TL: pre-training the weights for init purposes. Then use traditional gradient steps to update the parameters.
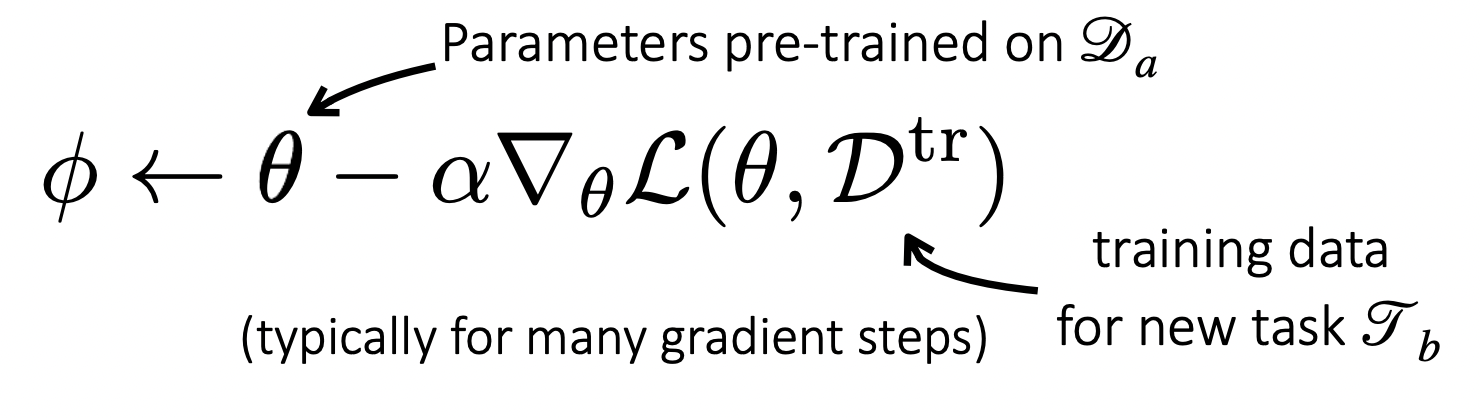
Idea is that you can pre-learn just general image features for example and then use this features when training on a new task. This applies for example, even when you pre-train using ImageNet for a medical image task.
- Question: criterion for when TL will work/helpful?
- Difficult, open question, some general common wisdom though (i.e., two medical tasks that are related… not hard rule though).
- Where to get pre-trained params?
- ImageNet
- Large language corpora
- Mathematical perspective: we have non-convex function we need to optimize. By pre-training, we can start in a better “basin” in the loss landscape.
Common design choices (common wisdom)
Above, we specified the general framework for pre-training/fine-tuning. But there exists many variants to this framework. The general idea is that we want to preserve a good balance of the old data while learning from the new data. In this sense, we can choose, for example, how many layers to freeze when training. Here are some common params:
- Motivation: typically you need to adjust the last layer for your task. This means we need to randomly init the last layer. However, during backprop, these random weights will “hit” the earlier layer weights and embed unwanted randomness into it. And for that reason, it might make sense to freeze the earlier layer weights so that we don’t override the valuable general features that we learned earlier.

Question: what is the difference between the above paradigm and self-supervised pre-training (e.g., using things like DINO and things like image puzzle occlusion)?
Question: do you need labels to pre-train for a target task that is supervised?
Where might the common wisdom break?
(Note: by common wisdom, we mean the things generally people do when TL’ing: e.g., freeze all layers but last, need diverse source dataset, etc.)
Here are some recent results:
- From the paper: “Unsupervised pre-training objectives may not require diverse data for pre-training.”
- Result was that you don’t actually need a diverse data set for pre-training (breaks common wisdom).
- Yoonho’s (TA) recent experiment
- We know that fine-tuning works well for only last layer. But why? last layer is really just like any other layer.
- Maybe for low-level distribution shifts, it might actually be better to only train a first layer and freeze the rest.
- Result: Fine-tuning the first or middle layers can work better than the last layers.
- Paper was released just last week! (Lee, Chen, Tajwar, Kumar, Yao, Liang, Finn. Surgical Fine-Tuning Improves Adaptation to Distribution Shifts. Openreview 09/28/22.).
Ok… wow lots of design choices then. Despite this, Chelsea recommends:
- Train last layer then fine-tune entire network
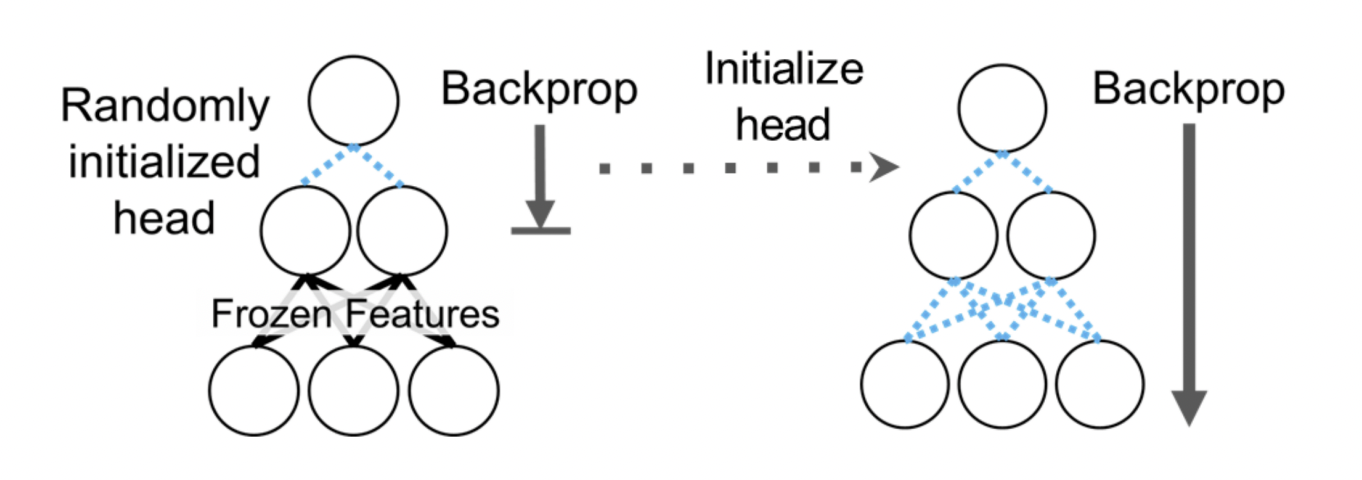
- And the idea is that we don’t mess up the earlier learned features by init the last layer to be within scope of the previous ones first before actually fine-tuning.
Major problem: Fine-tuning doesn’t work well with very small target task datasets. This is where meta-learning can help.
Meta-learning
We will cover: - Problem formulation - General recipe of meta-learning algorithms
Two views: mechanistic and probabilisitc.
Probabilistic ML
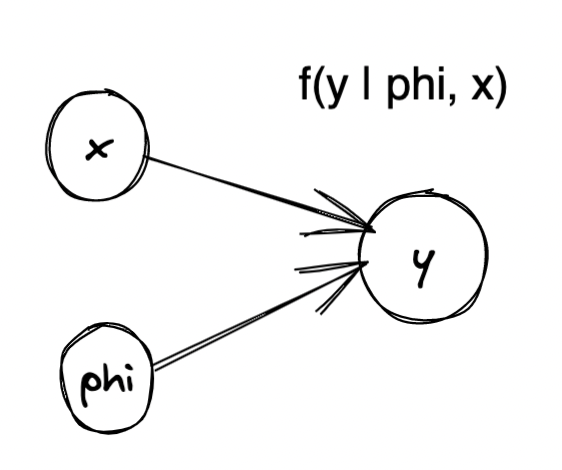
- Bayesian networks review: many random variables as nodes in a direct graph. \(P(y | x)\) (distribution) means \(y\) is dependent on \(x\) (not vise versa).
- Let’s now draw the graphical model for classic single-task learning.
- Now multi-task learning:
Mechanistic view
…