Constraint satisfaction problems

This note covers the units in CS 221 for the CSP unit.

I. Overview

Search but incorporating problem structure into the model and focusing on modeling instead of inference.

• Start of the variable-based models.
• Heart is object called a factor graph.
  • Will formally introduce them next lecture, but here is the general idea:

Definition 1 (factor graphs (high-level overview)): We are given a graphical model consisting of variables \(X_1,...,X_n\) and factors (functions) \(f_1,...,f_m\) where the factors defines how the variables relate to each other (in a graphical way):

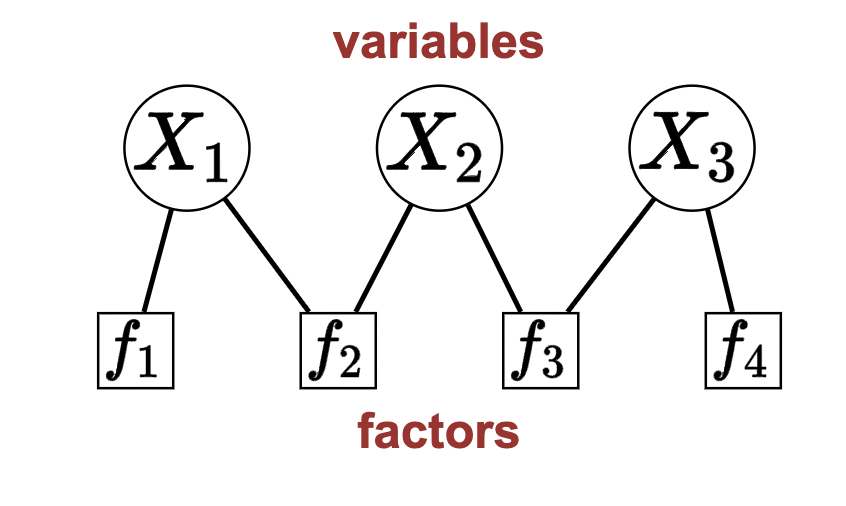
A solution to a variable-based model problem is an assignment to the variables (discrete or continious).

Here is an example:

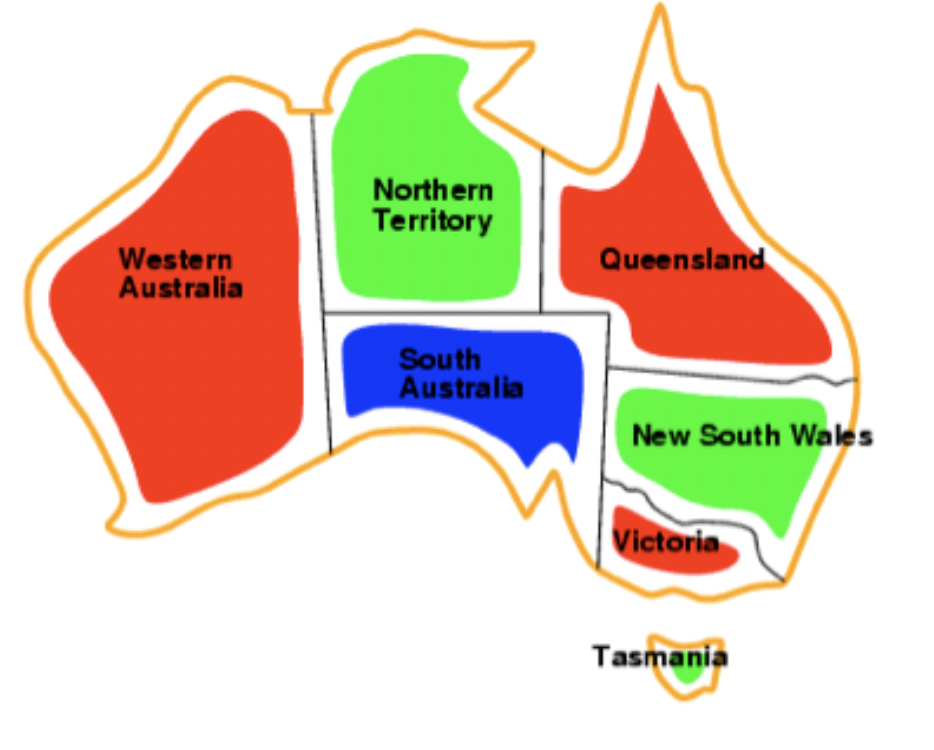
Example 1 (Map coloring): Given a map of Australia, color each of the provinces in red, green, or blue such that (the constraint) no two adjacent provinces have the same color.

To motivate factor graphs and CSP models, think about how we can solve this as a search problem. We can do it like this:

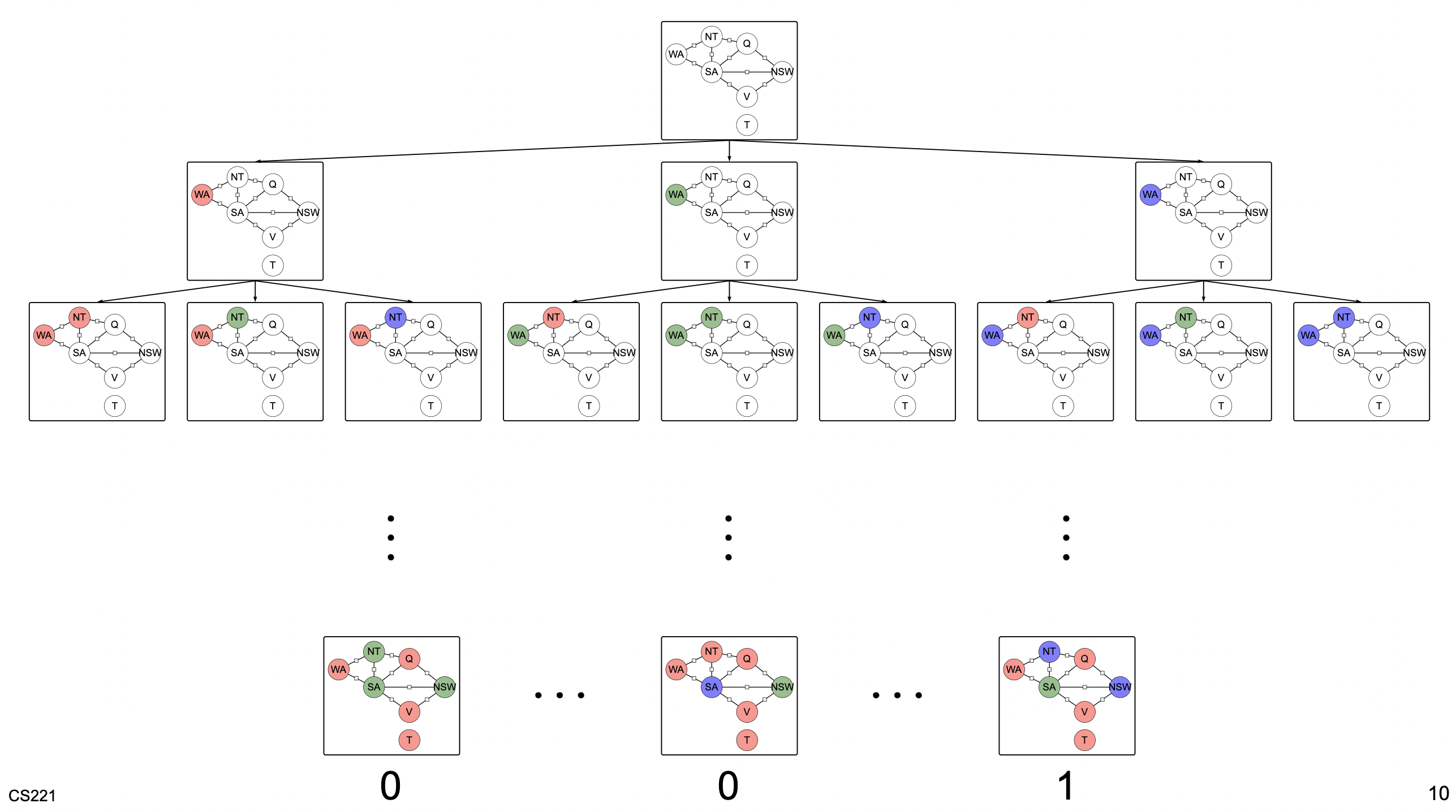
where each leaf node defines if it satisfies the conditions and each branch explores a potential solution path.

Key realization: the search problem doesn’t encompass useful information about the problem structure. For example, in this case:

• Variable ordering doesn’t affect correctness, can optimize
• Variables are interdependent in a local way, can decompose. That is, we can solve Tasmania in isolation cuz its in the ocean and then re-combine at the end to solve the entire problem. Decompose problem into subproblems.

The key realization is that by incorporating the problem structure into our solution (which search fails to incorporate), we can speed up the algorithm solution.

Variable-based models

• Algorithms:
  • Constraint satisfaction problems
  • Markov networks
  • Bayesian networks
• Key uniting factor:
  • Idea of a variable.
• Variable-based models is just another term for probabilistic graphical models!
• Theory is that variables are a higher-level (Python to assembly comparison) way to model a problems ❓.
  • Ok… this is what this means: we focus on modeling and devote the cumbersome work to the inference algorithms which allows us to focus more on modeling (unlike search). Makes more of a general framework to solve different types of problems unlike search.

So just to summarize, the idea behind state-based models is that we model the problem as a factor graph (modeling) and then assign values to the variables (inference).

Example problems:

• Vehicle routing: how to assign packages to trucks to deliver to customers.
• Scheduling: when to schedule sports team to meet to minimize things like travel, availability of TV networks, etc.
• School class scheduling

The thing that is ubiqitious about this is that we aim to solve an isolated problem but with a set of constraints (hence, CSP). As you might imagine, CSP’s are therefore very useful.

Roadmap:

• Definitions
• Algorithms to solve CSP’s
• Approximations to speed up the exponential cost

II. Definitions

From R&N:

To-do: cover weights.

Note: weights make you think globally (due to products in calculations) while factors represent local dependencies!

Note: factors == constraints.

Definitions (from slides):

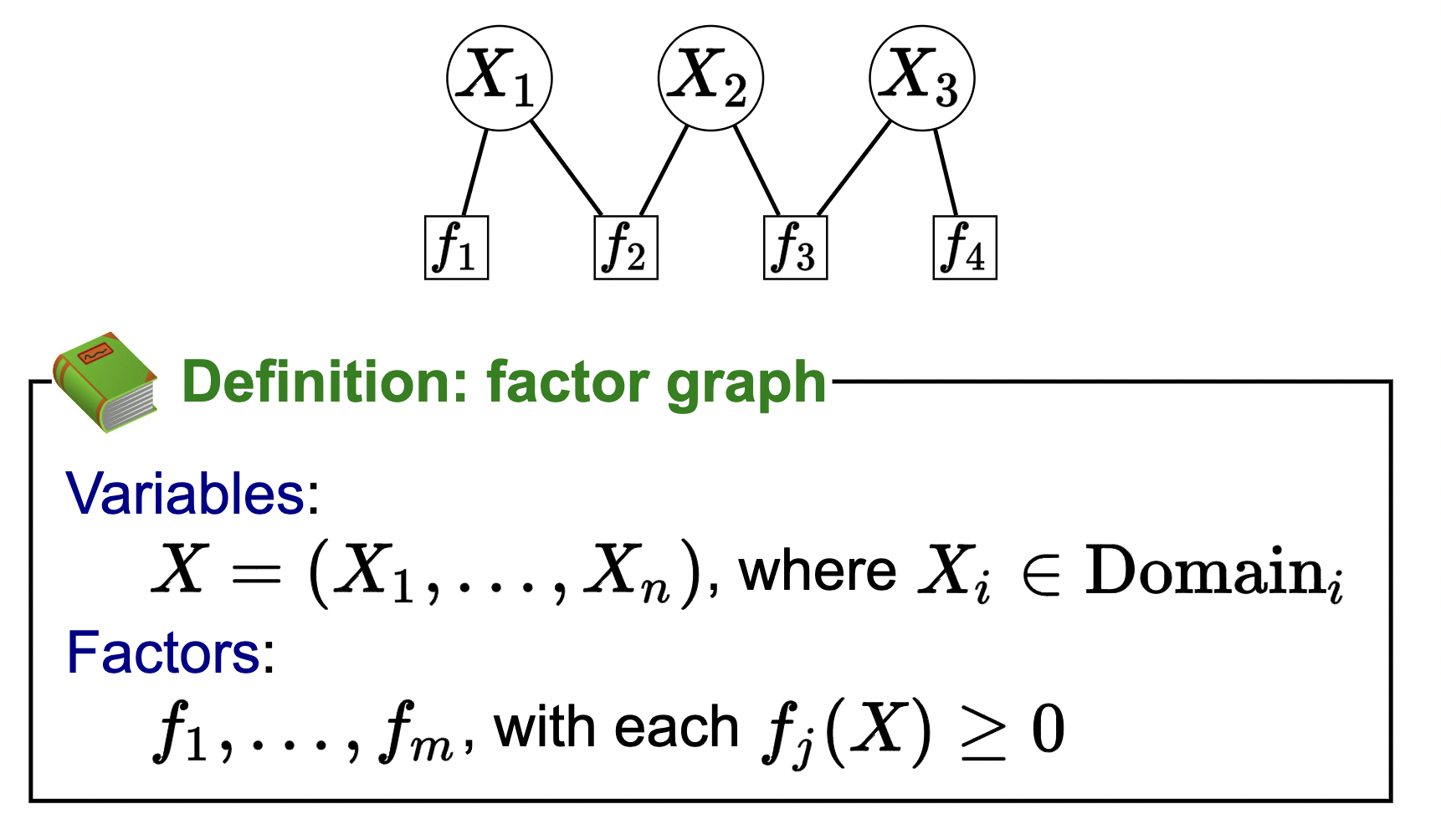
III. Examples

• LSAT logic puzzle
• Event scheduling
• Program verification

Definition 2 (indicator function): (useful for defining constraints/factors).

Can think of it as a python function that returns a boolean if the specified condition is true.

Basic idea is to formulate your problem in terms of variables (desired quantities to be assigned) and factors (your constraints for these variable values). A CSP will assign values to these variables that are supposed to satisfy the constraints. Moreover, define factors as indicator functions that check whether the specified condition (i.e., the constraint) is true.

IV. Dynamic Ordering

• We covered modeling, now let’s get to inference (how to solve CSP’s!)
• To understand how to solve CSP, must understand idea behind weights.

Each assignment \(x=\left(x_1, \ldots, x_n\right)\) has a weight: \[ \operatorname{Weight}(x)=\prod_{j=1}^m f_j(x) \]

(notice how it depends on the factors!) So essentially, what we are saying is that we set a weight for each factor/constraint and the outcome/result is what is being weighted. Then, we can mathematically define the objective:

\[ \arg \max _x \text { Weight }(x) \]

that is, find the max \(x\) for the assignments.

❓I guess the idea is that the solutions will have a bigger weight than non-solutions? What to do in tie? Where to draw line of solution and non-solution?

Backtracking search

• Blueprint for DO (dynamic ordering)
• Cut-off when condition isn’t satisfied
• Explore all paths
• Take highest weighted path at end as solution if satisfies conditions

We can probe this idea further to motivate DO.

• Idea: partial assignment weights
  • Recall that the weight of an assignment (solution!) is the product of all the factors.
  • We define the weight of a partial assignment to be the product of all the factors that we can evaluate, namely those whose scope includes only assigned variables.
  • For example, if only \(WA\) and \(NT\) are assigned, the weight is just value of the single factor between them.
  • When we assign a new variable a value, the weight of the new extended assignment is the old weight times all the factors that depend on the new variable and only previously assigned variables.