Lecture 26: Deep Learning

• DL is simply a bunch of logistic regressions stacked on top of each other.
• DL is basicaly MLE within neural networks.

\(P(Y|X=x)\)

How to train: - Apply MLE essentially.

Weights:

\[ \mathbf{h}_{j}=\sigma\left(\sum_{i=0}^{m_{x}} \mathbf{x}_{i} \theta_{i, j}^{(h)}\right) \]

Each individual weight calculation is simply a singular logistic regression.

Question: if each hidden layer neuron gets there input from the input vector, why aren’t all the hidden layers the same? Turns out MLE naturally diverges and initial params are randomly set.

So what is the parametric PMF? Turns out it is a Bernoulli.

• Prob distriubtion is literally at the end: Bernoulli for binary classification. We send in a data point and in the end it calculates the log likelihood that we see that data point.

Note:

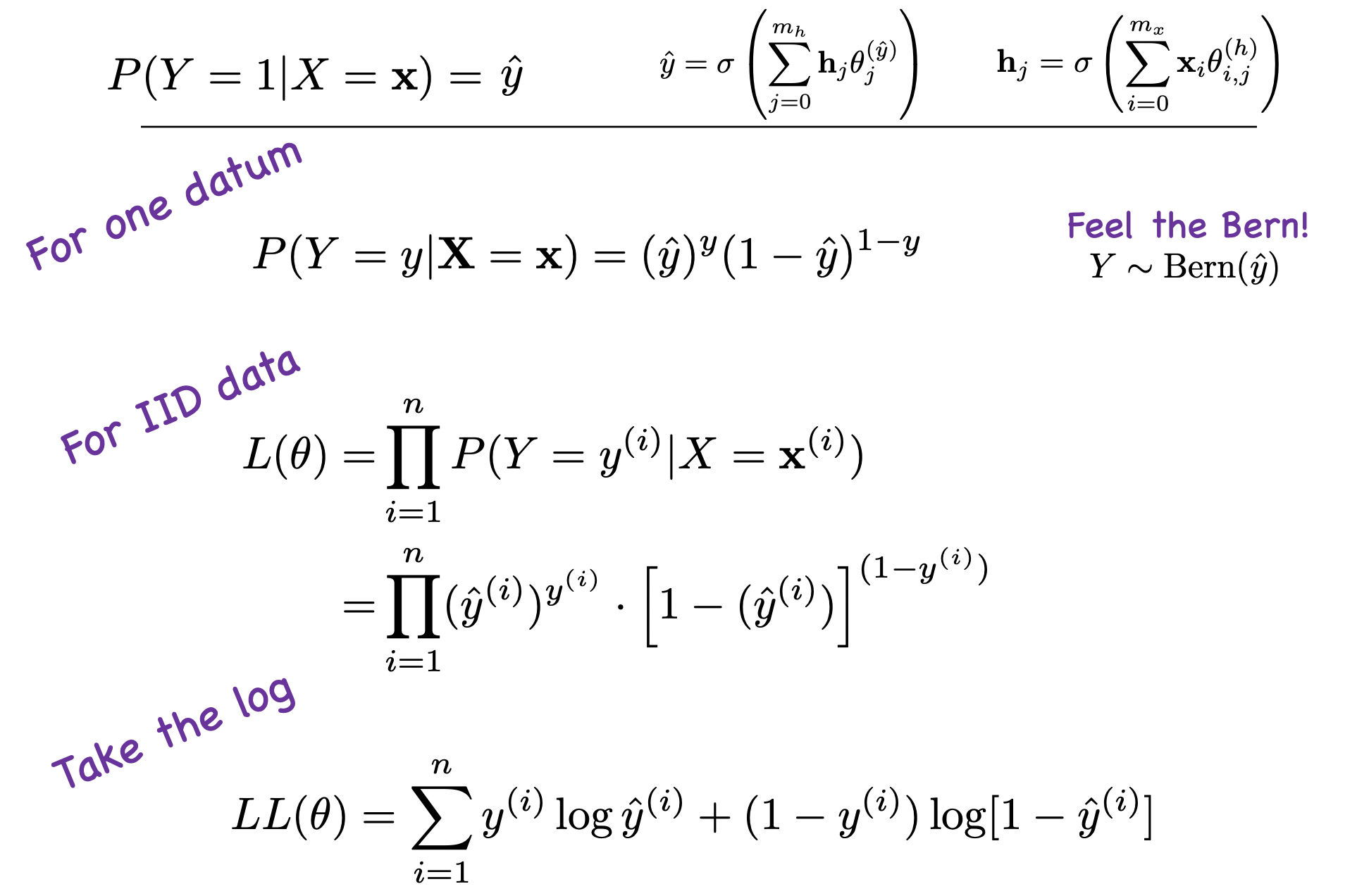
Each data point (or datum) goes through forward pass and you get a probability: \[ P(Y=y \mid \mathbf{X}=\mathbf{x})=(\hat{y})^{y}(1-\hat{y})^{1-y} \] Now do this for all data points and take the log

\[ L L(\theta)=\sum_{i=1}^{n} y^{(i)} \log \hat{y}^{(i)}+\left(1-y^{(i)}\right) \log \left[1-\hat{y}^{(i)}\right] \]

Train by calculating derivative of log likelihood with respect to all parameters.